INTRODUCCIÓN

En la naturaleza hay muchos movimientos que se repiten a intervalos iguales de tiempo, estos son llamados movimientos periódicos. En Física se ha idealizado un tipo de movimiento oscilatorio, en el que se considera que sobre el sistema no existe la acción de las fuerzas de rozamiento, es decir, no existe disipación de energía y el movimiento se mantiene invariable, sin necesidad de comunicarle energía exterior a este. Este movimiento se llama MOVIMIENTO ARMÖNICO SIMPLE (MAS)

El movimiento Armónico Simple, un movimiento que se explica en el movimiento armónico de una partícula tiene como aplicaciones a los péndulos, es así que podemos estudiar el movimiento de este tipo de sistemas tan especiales, además de estudiar las expresiones de la Energía dentro del Movimiento Armónico Simple.

 

EL MOVIMIENTO ARMÓNICO SIMPLE

Definición: es un movimiento vibratorio bajo la acción de una fuerza recuperadora elástica, proporcional al desplazamiento y en ausencia de todo rozamiento.

Solemos decir que el sonido de una determinada nota musical se representa gráficamente por la función seno. Ésta representa un movimiento vibratorio llamado movimiento armónico simple, que es aquel que se obtiene cuando los desplazamientos del cuerpo vibrante son directamente proporcionales a las fuerzas causantes de este desplazamiento.

Un ejemplo de este movimiento se puede encontrar a partir del desplazamiento de un punto cualquiera alrededor de toda la longitud de una circunferencia.

Cuando un punto (P) recorre una circunferencia con velocidad uniforme, su proyección (Q) sobre cualquiera de los diámetros de esta, realiza un tipo de movimiento armónico simple. Cada vez que el punto se encuentre en uno de los cuatro cuadrantes de la circunferencia, se trazará una perpendicular desde el punto a un diámetro fijo de la circunferencia. A medida que el punto escogido se mueve a velocidad uniforme, el punto proyectado en el diámetro, realizará un movimiento oscilatorio rectilíneo.

Para representar gráficamente (en una función) el movimiento armónico simple de un punto, se toman como abscisas los tiempos medidos como fracciones del período (T/12, T/6, T/4...) que es el tiempo que este punto tarda en dar una vuelta completa a la circunferencia; y como a ordenadas las sucesivas prolongaciones del mismo. La resultante es una sinusoide, ya que la variación del tiempo t, se traduce como una variación del sin x, donde x es el ángulo que forma el radio con el semi-eje positivo de abscisas (x es proporcional al tiempo).

 

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

 

Elementos:

1. Oscilación o vibración: es el movimiento realizado desde cualquier posición hasta regresar de nuevo a ella pasando por las posiciones intermedias.

2. Elongación: es el desplazamiento de la partícula que oscila desde la posición de equilibrio hasta cualquier posición en un instante dado.

3. Amplitud: es la máxima elongación, es decir, el desplazamiento máximo a partir de la posición de equilibrio.

4. Periodo: es el tiempo requerido para realizar una oscilación o vibración completa. Se designa con la letra "T".

5. Frecuencia: es el número de oscilación o vibración realizadas en la unidad de tiempo.

6. Posición de equilibrio: es la posición en la cual no actúa ninguna fuerza neta sobre la partícula oscilante.

Relación entre el M.A.S. y el Movimiento Circular Uniforme

El M.A.S. de un cuerpo real se puede considerar como el movimiento de la "proyección" (sombra que proyecta) de un cuerpo auxiliar que describiese un movimiento circular uniforme (­M.C.U.) de radio igual a la amplitud A y velocidad angular ω, sobre el diαmetro vertical de la circunferencia que recorre.

En lo siguiente podrás visualizar dicha relación.

Vamos a establecer una relación entre un movimiento vobratorio armónico simple y el movimiento circular uniforme. Esto nos va a permitir dos cosas:

- Hallar la ecuación del MAS sin tener que recurrir a cálculos matemáticos complejos.

- Conocer de donde vienen algunos de los conceptos que usamos en el MAS, como frecuencia angular o el desfase.

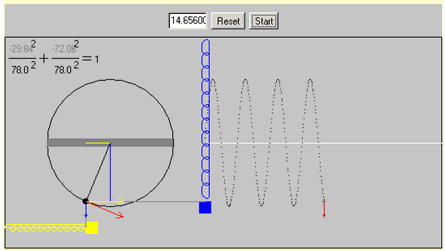
Observando el applet que viene a continuación. Tememos inicialmente el resorte azul, que oscila verticalmente. En la circunferencia tienes un punto negro que gira con movimiento circular uniforme, ocupando en cada instante una posición en la circunferencia. Traza mentalmente la proyección de esa posición sobre el diámetro vertical de la circunferencia. En cada momento, la masa que cuelga del resorte ocupa una posición determinada.  Observa que la posición de la masa del resorte coincide exactamente con la proyección de la posición del objeto sobre el diámetro, que verás en forma de línea azul en el diámetro vertical.

Es decir, como resumen, cuando un objeto gira con movimiento circular uniforme en una trayectoria circular, el movimiento de la proyección del objeto sobre el diámetro es un movimiento armónico simple.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Lo mismo podríamos decir del resorte amarillo y la proyección sobre el diámetro horizontal, que verás como un trazo amarillo sobre dicho diámetro.

Los vectores azul y amarillo, que varían en el applet, corresponden al valor de la velocidad del resorte, azul para diámetro vertical y amarillo para el horizontal. Observa su variación y comprobarás que la velocidad es máxima en el centro de equilibrio del resorte y mínima en los extremos, en los puntos de mínima y máxima elongación. Observa también como el vector rojo de la gráfica de la derecha, la velocidad del MAS, coincide con el vector azul, la velocidad de la proyección sobre el diámetro vertical, lo que supone una prueba más de lo que hemos afirmado anteriormente.

​

 

Ecuaciones del Movimiento Armónico Simple

Fórmulas:

​